Дана довільна множина символів. Потрібно побудувати всі можливі вибірки із даної множини без повторювань.

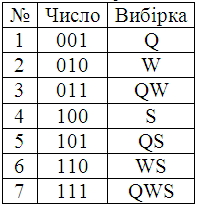
В умові задачі сказано, що вибірки повинні бути без повторювань. Це значить, що елементи, уже включені в чергову вибірку, необхідно якимсь чином позначити, щоб ненароком не включити їх до цієї вибірки ще раз. Елемент може перебувати в одному із двох станів – він входить у вибірку чи не входить до неї. Логічно елемент, включений у вибірку, відмітити 1, а той, що не входить до вибірки, відмітити 0.

Ідея розв’язання задачі. Складемо двійкове число із довжиною, яка рівна довжині вихідної множини, і тоді, якщо, наприклад, другий розряд двійкового числа дорівнює 1, то другий елемент множини бере участь у виборці, а якщо в деякому розряді знаходиться 0, то відповідний елемент множини у вибірці не бере участі. Тобто, задача отримання чергової вибірки зводиться до задачі отримання чергового двійкового числа із тих, які уже є. Отримати нове двійкове число можна звичайною операцією додавання двійкової одиниці.

Для того, щоб додати одиницю, достатньо знайти перший нуль, розпочинаючи із молодшого розряду, замінити його на 1, а потім всі одиниці, розміщені правіше (або лівіше, в залежності від того, де знаходиться молодший розряд) від тільки що поставленої, замінити на нулі.