У лівому нижньому кутку шахової
дошки m x
n стоїть шаховий король. Деякі клітини дошки заборонені для
відвідування королем. Король має змогу ходити або вправо, або вгору, або вгору
– вправо на одну клітинку. Знайти кількість можливих шляхів короля у правий
верхній кут дошки.
Ідея розв’язання. Задача є
класичною задачею динамічного програмування. Подамо шахову дошку у вигляді
двовимірного масиву розміром [1..n+1, 0..m] з
додатковими стовпчиком зліва і рядком знизу. Заповнимо усі клітинки масиву
довільним від’ємним числом, наприклад, -1, а клітинки додаткового рядка і
стовпчика, а також заборонені клітинки – 0. У клітинку старту занесемо 1.
Починаючи із нижнього лівого кутка, будемо заносити в доступні клітинки
кількість можливих шляхів, якими король може дійти до заданої клітинки, тобто
A[i, j] := A[i+1,
j] + A[i, j-1] + A[i+1, j-1]
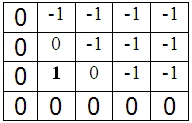
Малюнок, який ілюструє роботу
програми для випадку n=3, m=4, заборонені клітинки: (2; 1), (3; 2)