Дано прямокутник, довжини сторін якого А та В є натуральними числами. Скласти програму, яка знаходитиме, на скільки квадратів, сторони яких виражаються натуральними числами, можна розрізати цей прямокутник, якщо від нього щоразу відрізається квадрат максимальної площі.

Ідея розв’язання. Задача є класичним прикладом використання добре відомого алгоритму Евкліда, який ще називається «жадібним».

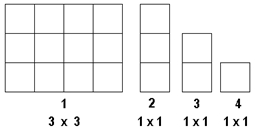
Очевидно, що сторона квадрата максимальної площі буде дорівнювати меншій стороні прямокутника (нехай А). «Відрізавши» цей квадрат від прямокутника (В=В-А), ми дістанемо новий прямокутник. До нового прямокутника застосуємо ту ж саму дію. Цей процес буде продовжуватись до тих пір, поки прямокутник не «виродиться» у квадрат.

Малюнок, який ілюструє роботу програми для випадку А=3, В=4

input.txt

output.txt

kvadrat.pas